統計学の専門家を名乗るとつげき東北氏が、なにやらシミュレーションをしたら「厳格な線引きができない条件下では、「萎縮」と表現規制が加速する」と言う結論が得られたと主張している*1。詳細は4980円を払わないと読むことができないので謎なのだが、前提条件に大きく依存している可能性が高いことは指摘したい。経済学部の1年生にも「うわ、単純すぎ」と思われてしまう仕掛けだが、恣意性はそう無い前提から、萎縮効果が強く出たり弱く出たりするモデルはつくれるから*2。
1. 基本設定
固定された費用Cを用いて、過激さaの作品をつくる合理的なクリエイターを考えよう。クリエイターの効用はU(a)-Cとする。U(a)は金銭換算した作品を公開することで得る効用。このクリエイターは過激であれば過激なほど効用が高まるとして、 ∂U(a, C)/∂a ≥ 0を仮定する。こういう状況で、aが大きいと法規制をされる場合と、高確率で世間からの非難を浴びて作品を撤回する場合を考えよう。
2. 法規制をするケース
ベンチマークとして、aが大きく閾値hを超えると法規制をされる場合を考えよう。規制の内容は検閲で作品を公開したり、売ったりできなくなるとする。このときのクリエイターの期待効用関数は、
となる。法規制の場合はhは非確率変数とする。クリエイターはE[Uᵣ(a, C)]を最大にする作品を作成し、そのときのaをâと書くと、â=hとなる。
3. 自主規制をするケース
自主規制を定義するのは厄介なのだが、便宜的に世間からの非難を浴びないように振舞うことを自主規制とする*3。 aが大きく閾値hを超えると世間からの非難を浴びて、作品撤回に追い込まれることを考えよう。自主規制の場合の閾値hは確率変数で、クリエイターは作品製作時に実現値は知らない。ただし、その確率密度関数f(h)は既知とする。hがaよりも大きくないと作品公開による効用を得ることができないことに注意すると、このときの期待効用関数E[Uₐ(a, C)]は以下のようになる。
F(a)は累積分布関数で、確率密度関数を区間(-∞,a)で積分した確率を表す。微分積分学の基本定理を思い出しつつ整理すると、aの最適化の一階条件は以下になる。
クリエイターが選ぶ点âは、U(a)とf(h)次第と言うことになる。
4. 法規制と自主規制の比較
法規制に対して自主規制が過剰に萎縮するかU(a)とf(h)を具体的に特定した上で検討しよう。
もっとも単純な効用U(a)=aを考える。法規制の強弱など如何様にもなるので、hの期待値が同じとする。f(a)は定義域が非負のガンマ分布*4を仮定し、形状母数κと尺度母数θを期待値E[h]=0.5になるように置く。 θ=0.5/κとなり、分散はκ(0.5/κ)²となる。このとき形状母数κと過激さaの関係をプロットすると以下になる。
分散を世間から非難を浴びるかいなかの曖昧さとすると、κが小さいほど分散が大きくなるので、分析したκの区間では、非難を浴びる基準が不明確な方が自主規制が緩くなることが分かる。「厳格な線引きができない条件下では、「萎縮」と表現規制が加速する」とは言い難い。まぁ、κ→∞で法規制と一致するとは思うが。
形状母数κ次第で法規制よりも厳しく自主規制(â<0.5)する萎縮効果も、緩く自主規制(â>0.5)される効果も生じることになる。奇妙に思われるかも知れないが、U(a)(1-F(a))=a(1-F(a))を最大化するaをâとして選んでいるので、累積密度関数F(a)の形状によってâは動くのだ。以下の2種類のκのプロットにおいてはa(1-F(a))は面積になるが、ぐにゃっと曲がった関数を所与に面積最大化するので奇妙なことが起きるのが分かる。
クリエイターの効用関数をもっと現実的なモノにできて、非難を受ける閾値の確率密度関数をもっと現実的なモノにすると言うか、せめて形状母数κが推定できればもう少し確定的なことが言えるのだが、どちらも自明な議論があるわけではない。
なお、実際には法規制を避けるために、業界団体が自主規制を提案するものだ。例えば、出版4団体でつくった出版倫理協議会が自主規制を行いつつ、条例制定反対運動に従事してきた。つまり、業界団体は自主規制の方が自由度が高くなると判断している。
5. 理想状態がわかっているならば法規制の方がよいが
上の議論においては、社会に最適な閾値がわかっているならば法規制の方がよいと言うことになる。自主規制は過少か過剰かになりがちなので。数理モデルなくして分かる自明の話だが。ツイフェミの皆さんは最適な閾値が自明のように言うので、法規制の方がよい蓋然性は高いかも知れない*5。
ただし、これも状況次第。つくられた作品に事後的に非難を浴びせるしかない場合もありえる。文化的に許容される過激さが変化する場合で最適な閾値がわかっていない場合や、過激さが露出度や恥部の描写の有無など一次元の値にできない場合などは、不完備性と言うか適切な法文が書けない。ヘイトスピーチ規制の議論では、問題表現が可視化されるようにすることにより、人種差別の程度を把握できるようにするべきと言う議論もあった*6。
6. まとめ
物理学であればよく知られた基本方程式の信頼性が高いので、説得的な前提を考えなくても確度の高い前提をもとにシミュレーションができるのだと思うが、社会科学分野ではそんなことはできない。とつげき東北氏の結論リストを見ると、時間経過や抜け駆けの問題も分析したことになるが、どれだけの仮定を積み上げているのか、それらの仮定をどれだけ正当化しているのか。
そもそも自主規制とは何なのかと言う哲学的な用語定義の問題を片付けないといけない。クリエイターの良心に働きかけて、クリエイターが罪悪感を感じないように自主規制する場合は、自主規制に過剰は定義的にないし。数理モデルをつくってシミュレーションする前にやるべき作業はいろいろとあるし、やるべき作業をやったらわざわざ数理モデルをつくるまでも無いかも知れないことは、頭の片隅に残しておいて欲しい。
*1【自主規制は損!】いかにダメかを、数理科学的に証明してみた(表現規制版)|とつげき東北|note
*2常識的で説得的な前提から意外な定性的な傾向を示せれば学術論文になるので、普通に議論したらどっちつかずの話になる。
*3法規制に従っている場合は非難を浴びない前提になっているが、法規制に従っていても非難を浴びうるとする場合は、以下のモデルで分散の小さい(κの大きい)状態を法規制がある場合と見なせばよい。
*4ガンマ分布は指数分布やχ二乗分布(の変形)を一般化していて、かつ再生性を有する。また、消費者ごとの購入頻度の分布がガンマ分布に従うことが経験的に知られており、社会の中で観察することもできる。
*5関連記事:法規制ではなく自主規制で女性表現を制限すべき理由を捻り出すのは難しい
*6関連記事:ヘイトスピーチの非合法化には反対




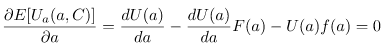








0 コメント:
コメントを投稿