ベイズ統計学の「小さな世界」は、ベイズに限らずあらゆる計量分析に当てはまる特徴だよ

高名な情報量規準主義者の主観ベイズ統計学への誤解を受けてか、統計学を専門としない数学者が、ベイズ意思決定理論における小さな世界（small world）と言う特徴を3年間ぐらい繰り返し批判している^*1。しかし、ベイズ以外のあらゆる数理的分析においても小さな世界を分析することになるので、殊更、ベイズ統計学の欠陥のように取り上げるのはミスリーディングだ。

NENENENE＠研究さんの「女子枠」批判論文の統計解析は、参照している記事で論文が批判しているはずの女子枠推進者の主張の検証になっていないし、分析手法の選択が下手な上に、解釈におかしいところがある

NENENENE＠研究こと國武（くにたけ）悠人（ゆうと）氏の女子枠批判論文Kunitake (2025)には、統計解析をかけている部分があるのだが、女子枠推進者の主張に対応していないので意味をなしておらず、手法の選択が下手な上に、解釈がおかしいところがあるので指摘したい。

これから研究を学ぶ大学院生が、半年前とは言え学部生のときに書いたペーパーを批評するのは心苦しいが、学術論文として公刊してしまったのだから仕方が無い。気づくと週刊誌に記事を書いているし、社会的影響力も出始めている。

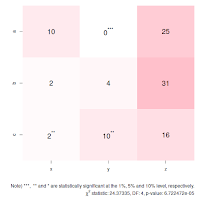
統計学教育の苦しいところ — 統計学ユーザーの皆さん、クロス表の独立性検定の統計量がなぜχ二乗分布に従うと看做せるか説明できますか？

「クロス集計表を作るのは簡単だけれど、カイ二乗検定の説明になると難易度が数段上がってしまう」と言うツイートを見かけた。まさにその通りで、クロス表の独立性検定はよく見かける一方で、その説明は難しい。

クロス表は二種類の因子の組み合わせごとの度数をまとめた表のことで、独立性検定とは二種類の因子に相関が無いと言えるかを調べる方法だ。共変量を統制できないので効果的に利用できる場面は限られるが、入門レベルの教科書や学部の講義ではよく紹介されている。

埼玉県警が県議会で証言した外国人検挙者数には、出入国管理法違反やインバウンド客の迷惑行為が含まれているよ

これまで名誉毀損で何回も問題になり、虚構を含めた情報を拡散させるなどしてクルド人への憎悪を煽っていると非難されている、ジャーナリストの石井孝明氏が出した埼玉県の外国人検挙率の数字を参照し、「リベラルや反差別を掲げる人々」は「統計的根拠に基づいて差別をすることを肯定するべきかどうか」「答えなければならない」と主張しだした人がいるのだが、その前に石井孝明氏の出した数字がミスリーディングなものでないか検討する必要があるので指摘したい。

ここ数年でフェミニズムが急速に支持を失ってきたということはないよ

SNS男女論界隈では、ここ数年でフェミニズムが急速に支持を失ってきたと言うような主張が、フェミニズム批判者から見られることがある。𝕏/Twitterでの議論では勢いが無くなっているようだ。しかし、日本全体で見るとそう大きな変化はない。

世論調査の結果を参照して、男女共同参画推進派フェミニストが数を減らしているという主張もあったりするのだが、これは解釈に難がある。

Rによる統計解析をシステムに組み込むのは、言うほど非現実的ではないよ — メッセージ・キューを使えばね

「R言語は本当に実装向きではないのか？— 固定観念を問い直す」と言う記事を見かけたのだが、シングルスレッドだからシステム構築に向いていないと言う主張がされていた。Pythonのウェブアプリケーションもシングルスレッドで使われているわけで、話がおかしい。恐らくシステム構築に関わったことが無い人が書いている。

質的調査で「仮説」が検証できるまで調査対象者を増やすのは研究不正にあたるのか？

社会学の質的調査（インタビュー）^*1では、仮説が検証できるまで調査対象者（インタビューイ）を増やしていくと言う説明があり^*2、𝕏/Twitterで統計学的に不正だと非難されている。

社会学者がやっていることなので胡散臭く思うわけだが、その非難は的を外している。サンプルサイズを適応的に増やすことが直ちに統計不正になるわけではないし、そもそも質的調査は事例研究に過ぎず、統計解析から普遍的な傾向を示すものではない。またインタビューイを増やすことが、標本調査のサンプルサイズ拡大にあたる行為とも限らない。

財務省のデータ解析が不適切だと批判しているデータサイエンティストの外れ値の処理が良くない件

財務省がOECD諸国の一人あたり実質GDP成長率を歳出拡大率に単回帰をかけて、両者に「相関が無い」と主張したことに対して、本業はデータサイエンティストとのことのhatankokka氏がデータ解析が不適切だと批判し、外れ値を除外した異なる分析を提案している^*1。

しかし、どうもhatankokka氏は、財務省の意図をよく理解していない気がするし、また、代わりに提案している分析も適切とは思えない。問題に気づいていない人々がいるので指摘しておきたい。

メディアの皆さん、中高生の自由研究を世に広める前には

それを専門とする研究者のコメントをもらってください。

動画の高速再生がどの程度視聴者の理解を困難にするかについての高校生の研究を、インタビュー型式で紹介したウェブの記事^*1が話題になったのだが、藤田医科大学の宮川剛氏が提示されたデータからそのような事は言えないのではないかと𝕏/Twitterで批判しだし^*2、学校に詳細を問い合わせるなどを行った。そして、この宮川氏の行為に賛否が議論になっている。

データ可視化も使いよう — 変化を促すのに役立てられるよ

ナイチンゲールがクリミア戦争の死因の分析の説明に鶏冠図（polar-area diagram）を用いた^*1時代から有用性が知られるデータ可視化が、企業の意思決定に目立った貢献がなく、もう流行っていないように見えるのは何故かという考察が話題を集めていた。

これはデータ可視化の問題と言うよりは、BIツールのダッシュボードの問題であろう。BIツール導入事例紹介を見ると、以前から集計していたはず^*2の数字を綺麗に表示しているものが多く、無意味と言うことは無いが、目新しさはない^*3。手間隙の削減はともかく、見せている数値は同じだ。当然、企業活動の変化は考えづらい。

性的児童虐待の被害を受けると、成人後に性的児童虐待を犯しやすくなるとは言えない

Salter et al. (2003)を紹介している日経メディカルの記事に参照しつつ、性的児童虐待の被害者は、性的児童虐待を犯しやすいと主張している人がいた。あるイギリスの総合教育病院にかかった家族外からの児童性虐待の被害を受けた224名の男性のうち26名が、後日、家族外に児童性虐待を行っていたことを指摘する論文だ。他にも、Ogloff et al. (2012)はオーストラリアのデータから相対リスク7.59としている。これらの論文からは、性的虐待の被害者は明らかに高リスク群に思えてくる。

NHK高校講座の数学Ⅰの統計的仮説検定に関する理解度チェック問題は、母平均の検定を念頭に置いていない蓋然性が高い

NHK高校講座の数学Ⅰの統計的仮説検定に関する理解度チェック問題が、間違っているのではないかと話題になっている。

統計的仮説検定では、分布のパラメーターがある値である等号の式を帰無仮説としてとることが多く、片側検定の場合は不等号で表記することもあるといった慣習なのだが、不等号の帰無仮説のみを正解としているからだ。

平均代入法による欠損データ処理はオワコンどころか黒歴史なので

野村総合研究所の塩崎氏と広瀬氏の記事^*1がまた^*2データ分析者に困惑を引き起こしている。「データが欠損している場合は、平均値や中央値で埋め合わせる作業を行います。」とあるのだが、欠損データ処理としてはよくない手法として知られている。

誤差項の分散に不均一性があるパネルデータにもOLSは使えるよ

社会学者の柴田悠氏の社会調査協会の『社会と調査』第17号に掲載されたエッセイ「政策効果の計量分析—一階階差 GMM 推定の手順と実際」の話の頭に、パネルデータ分析に慣れていない人を混乱させそうな誤解が書いてあったので指摘しておきたい。

「パネルデータには OLS推定を適用できない…前提諸条件のうちの2つが…成立しない…1つは，誤差はどの国でも均一に生じるという条件…1つは，どの国のあいだをとってみても誤差の相関がないという条件」とあり、個体方向もしくは時系列方向に誤差項の不均一性があるパネルデータには最小二乗法（OLS）が使えないと言う主張がされているが、有効ではなくなっても、不均一分散以外がOLSの仮定を満たせば、不偏かつ一致する推定量が得られるので、あとは標準誤差の計算に一手間かければ問題なく使える。

理工系ラボの皆さんにお勧めしたい統計手法

理工系のラボの統計解析では実験計画をどうするかの方が成果を大きく左右するためか、出てきたデータの統計解析はよく考えずに慣習に沿っている面がある。国内外の理工系ラボの向けの実践ガイドライン（チートペーパー）を見ると、古臭く問題含みの方法を説明していることもある。

信頼区間を説明する前に知っておくべき変態的な例

推定された信頼区間を母集団のパラメーターが95%の確率で入っている区間と説明するなんちゃって解説はよくされており、昨日も中堅私大のマーケティング分野の大学教員がウェブ媒体でそのような説明をしていた。しかし、観測値から実際に計算された信頼区間は、母集団のパラメーターがある確率で含まれる区間ではない。

ややこしいので世界中で勘違いされている信頼区間だが^*1、理解を深めるための変態的な例であるWasserman (2010)の6.14 Exampleを紹介したい。Berger and Wolpert (1984)が元ネタと書いてあるので、恐らく語り継がれている有名な例。

マン=ホイットニーのU検定（ウィルコクソンの順位和検定）と中央値

t検定やF検定を使う事が多いので、マン=ホイットニーのU検定（ウィルコクソンの順位和検定）を使った事は無かったのだが、心理学や生物学方面ではよく使われているようだ。しかしこの検定、世界的に定義や性質が誤解されながら運用されてきている。

昨日も、あるU検定の説明は誤りだと言う指摘に続けて、不正確な説明がされるのを見てしまった^*1。

野村総合研究所データサイエンスラボの人々が描いたポジショニングマップ

野村総合研究所データサイエンスラボの偉い人が「令和の｢データサイエンティスト｣に必要な能力」と言う記事を書いて、その中の「統計学や機械学習における基礎的な知識・スキルを整理してマッピングした…図」が、統計学や機械学習に詳しい人々の困惑を招いている。

p値の大小からももちろん、統計的有意性の強弱を言うのをそもそもやめましょう

エーザイの内藤晴夫代表執行役CEOが、アルツハイマー病治療薬の治験で「主要評価項目に据えた「投与開始から18か月時点のCDR-SB」は、p値が「0.00005」となり、「私も長い間この仕事に携わっているが、このようなp値を見たのは初めて。非常に高い統計学的有意性と言えると思う」と有用性を強調した」事で^*1、SNSの統計学クラスターがざわついている。

210本安打を記録した1994年のイチロー選手の試合ごとのヒット数がポアソン分布に従わないのはアタリマエ

「イチローの安打数がポアソン分布にならず正規分布になる理由を考察してみた」が流れてきた。曰く、1994年のイチロー選手は打率が高く好不調の波が小さいので、その試合ごとのヒット数はポアソン分布では無く正規分布に従っていると主張されている。分析と解釈に色々と問題があるので指摘したい。